こんにちは、山口むつおです。

 

みなさんはスナック菓子の「ポリンキー」をご存知でしょうか。

 

 

 

 

 

本日3月3日はポリンキーの日だそうです。10年以上振りくらいに食べてみたら、その間ずっと味の改良が行われていたらしく、子供の頃に食べた時に比べてびっくりするくらい美味しくなっていました。マジで。

 

 

そしてポリンキーといえば、「三角形の秘密はね♪」「教えてあげないよ、ジャン♪」のTVCMですよね。

 

 

 

 

 

25年たった今でも、ず〜〜〜っとこの「三角形の秘密」を教えてくれないんですよね……。

 

 

 

 

 

 

 

「ポリンキー　都市伝説」と検索すると……。

 

 

 

 

 

 

 

検索結果の中に……。

 

 

 

 

 

 

 

「ポリンキーの三角形の秘密を探ってた友人が死んだ」というネタのスレが2chで立つ始末。WEB上でも何かとネタにされるほど、ポリンキーの三角形の秘密はオモテに出てきてないのです。

 

そこで……。

 

 

 

 

 

 

 

めちゃくちゃ頭のいい人に協力してもらい、三角形の秘密をマジで当てにいきたいと思います。

 

 

 

 

 

 

情熱大陸にも出た、カリスマ数学教師が降臨

 

 

お話を伺ったのはコチラの方！

 

 

 

 

 

 

柳谷 晃（やなぎや あきら）

 

日本の数学者、作家。早稲田大学高等学院数学科教諭、早稲田大学理工学部兼任講師、早稲田大学複雑系高等学術研究所研究員。専門は微分方程式とその応用。

早稲田大学理工学部数学科卒業、同大学院理工学研究科博士課程修了。

 

※Wikipediaより抜粋

 

 

先生が教えている早稲田大学高等学院では「神」として崇めている生徒も多く、なんと情熱大陸にも出たこともある、超人気の数学教師です。

 

 

数学のカリスマ教師…！本日は宜しくお願いします！

 

 

はい、宜しくね！

 

 

早速、ポリンキーの三角形の秘密について見解を聞いていければと思うのですが……。

 

 

まず三角形についてちょっと考えてみましょうか。ポリンキーはどういう三角形なの？

 

 

えーと、ちょっと待ってください……。

 

 

 

 

 

 

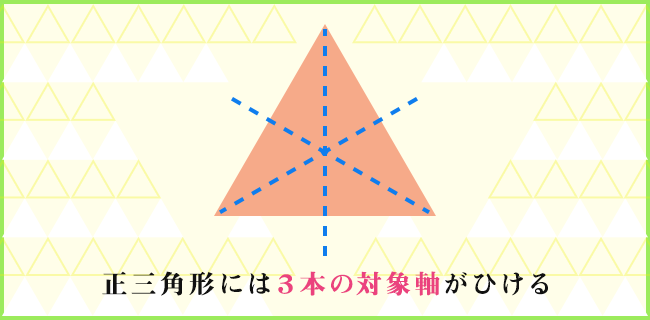
全部の角度が60°だから、正三角形ですね。

 

 

正三角形の性質は、すべての角が60°、そして3本の線対称の軸が引けるよね。

 

 

 

 

 

 

 

 

線対称というのは、心理的に高貴な印象を与えるんだよ。菩薩像なんかは、服のひだまで左右対称に作られているものが多く見つかっているんだ。言い換えると、ちょっと近寄りがたい印象を与えるってことだね。

 

 

なるほど。

 

 

それで僕は、顔が線対称の芸能人は人気が出にくいという持論を持ってるんだ。だからほら、ちょっと前のにブレイクした女優の◯◯◯さん。彼女なんて、顔面のパーツ配置がめちゃくちゃでしょ？

 

 

？！

 

 

あのアイドルグループの△△△△さんも、顔のバランスが崩れてるからいいよね〜！

 

 

あ！あのモデルのXXXXさんは顔が線対称だから、人気ないよね。

 

 

ほら、あの大人気アイドルの子！パッと見、線対称の顔をしてるでしょ？でも横からみたらアゴがすごくてさ〜！

 

 

書けるかこんな話！！！！！

 

 

 

 

 

うふふふ……！

 

 

先生、芸能人の悪口は書けないのでマジでやめてください。話を戻すと、じゃあポリンキーは親近感がわかなくてダメってことじゃないですか？？

 

 

さっき言った高貴さは、対象物が大きな物の場合に感じる感覚なんだよね。お菓子のような小さなものであれば、高貴が清潔、綺麗が美味しそう、という気持ちを呼び起こす可能性がある。それを狙ったんじゃないかな。

 

 

 

 

 

 

 

 

 

自然界に存在する「黄金比」「フィボナッチ数列」が不思議すぎる

 

 

線対称は高貴に感じるって言ったけど、数学的に人間が最も美しいと感じるものの1つに「黄金比」というものがあります。

 

 

ジョジョの奇妙な冒険に出てきたので知ってます！自然界や建築によく見られるっていうアレですね。

 

 

 

 

 

 

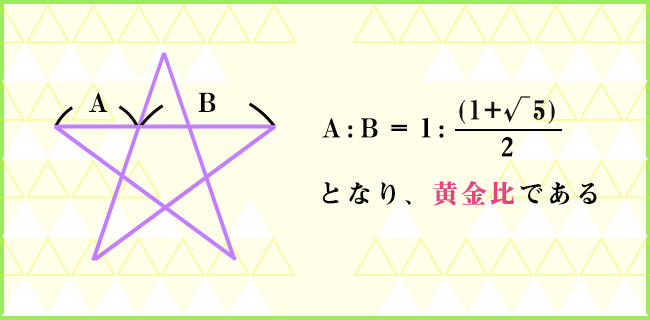
そう。この性質を含んだ身近な形として五芒星…いわゆる星形があるよ。

 

 

 

 

 

 

 

 

確かに、星形はみんな好きですもんね。

 

 

この黄金比が自然界にあらわれているものの代表として、植物の葉の付き方がある。植物の葉はなるべくたくさんの太陽光を受けるために螺旋状に葉をつけるんだけど、その順番が黄金角になってるんだ。黄金角っていうのは、円周360°を黄金比で分割した、狭い方の角度のことね。

 

 

 

 

上の葉っぱの影にならないように効率的な葉の位置をシュミレーションしていくと、360°を黄金比で割った角度＝黄金角が出現。なんで？？
※写真はロマネスコの葉

 

 

もう1つ自然界に存在する不思議な数学があって、フィボナッチ数列というものがあるんだ。こいつの数字の並び方は、自然界のあらゆるところに登場するんだよ。

 

 

 

 

 

 

 

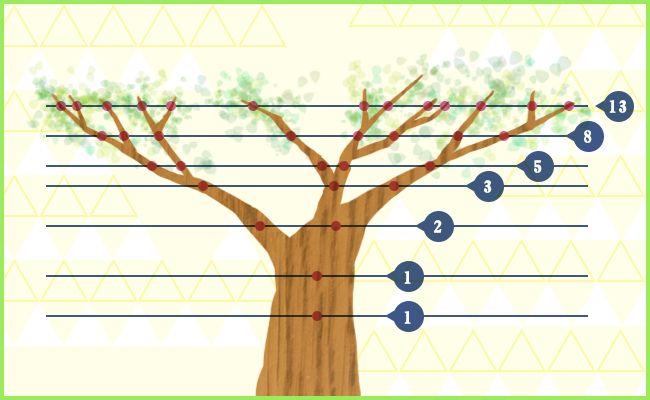
例えば木の枝。木の枝は成長するにつれて枝分かれしていくけど、あれは全部フィボナッチ数列のルールで枝分かれして成長するんだよ。

 

 

 

 

 

ん？いま全部っておっしゃいましたけど、世の中の木、全部ですか？？

 

 

 

 

 

うん、全部。

 

 

 

 

 

この世のほとんどの木が、フィボナッチ数列と同じルールで1本、1本、2本、3本、5本、8本、13本……と枝分かれしていく。なんなのそれ！

 

 

 

 

不思議すぎるわ……。

 

 

さらに不思議なことに、このフィボナッチ数列、隣り合う数字で比を作っていくじゃない？
1:1, 1:2, 2:3, 3:5,……って感じで。これを無限にず〜っと繰り返していくと……

 

 

 

 

 

……という感じで、黄金比に収束していきます。

 

 

不思議すぎるんで、死んだら神様に理由を聞いときます。

 

 

 

 

 

 

ポリンキーを三角形にするための製造方法は？

 

 

 

 

ついでだから、どうやって三角形にしてるかも考えてみようか。実はポリンキーに空いてるこの穴、よく見ると一辺のだけ、辺をまたぐように穴が空いていることに気づいた？

 

 

 

 

 

 

 

 

つまりどういう事ですか？

 

 

これはもともと穴が空いている生地を折り曲げて、正三角形にしてるって事じゃないかな？折り曲げて正三角形になる形……つまり、菱型（ひしがた）だね。

 

 

 

 

 

穴の空いた大きな生地に対して、並行にカットした後……。

 

 

 

 

今度は並行な線に対して60°の角度で、並行かつ等間隔にカット。そうする事で一気に大量の菱型の形を作っているんじゃないかな。
そして最後は折りたたんで、真ん中だけオイルでも塗ってくっつかないようにし、揚げれば今の形になると。

 

 

 

は〜〜〜、なるほど！

 

 

 

 

 

まとめると、ポリンキーを「三角形」にしようと思った時に、製造コストを考えると菱型から正三角形にするのが最も効率的だった…という事なんじゃないかな？？

 

 

けっこうリアルな仮説ができたな〜。先生、ありがとうございました！

 

 

 

 

 

 

 

 

 

 

 

 

 

……というわけで、仮説は立ちました。この仮説は合っているのか？湖池屋に直接ぶつけてみたいと思います。

 

 

 

 

 ▶いよいよ湖池屋に「三角形の秘密の仮説」をぶつけに行きます。