オモコロ

海辺の街……

 

 

 

美しい景色だ、とは分かる。
＿＿だが心が動かない。

 

だから私は28年の人生に終止符を 打とうと思う。でも……その前に

“走馬灯”が見たい。

 

 

 

死の間際に見るという “走馬灯”……

 

走馬灯とは、

死の間際、その人生の全てを、
もう一度振り返り再体験するという臨死体験。

 

 

 

 

一歩踏み出せば、地面に叩きつけられるまでの間に、走馬灯を見るはずだ。

 

 

 

ほんとうに……？

 

崖から地面まで、２秒か３秒か、
走馬灯が、ビデオの早送りのようなものだとしても、
そんな短い時間で、人生の回顧録が全て再生できるだろうか？
 

例えば、再生時間が足りなくて、いいところで走馬灯が終了 するなんて絶対にイヤだし、

逆に、時間が余ったらどうなる？
スタッフロールとともに自分の 人生のNG集 でも見させられるのか？ 

もともとNG集みたいな人生のNG集 を？
そいつもゴメンだった。

 

自分の走馬灯の再生時間を確実に知る必要がある。
そして、その再生時間に見合った、崖の高さもだ。

 

 

 

 

飛び降りる前に考えてみる。

 

走馬灯の説明に、魂や神を持ち出さなくともよい。
ようは、特殊な条件下での 脳の働き なのだ。
たとえば「夢」や「瞑想」で、私たちは「ありもしないもの」を見る。

 

かのアイルトン・セナはこう言っている。 

“わたしたちの脳は、自身の体験を全て記憶している” と。

 

 
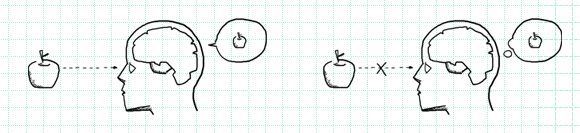
人は目で見て耳で聞くばかりではない。脳の記憶を見て聞くこともできる。

 
「特殊な条件下」とは、ここではもちろん「死を悟る」ことだ。
死を覚悟した脳は高速化し古い記憶を呼び戻し甘美な幻覚をわたしたちに見せる。

それが 走馬灯の正体だ。

そして死の覚悟は、崖から一歩踏み出したときに始まり、地面に激突したとき、脳が停止して消えるはずだ。

つまり、落下中に走馬灯を見る。
言い換えれば、落下と走馬灯の時間は重なっている。

 

 

 

 

　「走馬灯を見る時間＝落下時間」

 

これをふまえて、落下時間を求める。
ここからはしばらく物理学だ。

興味がなければマウスホイールをガーッ と下までやってほしい。

 

人体は複雑な形状をしているため空気抵抗を受ける。
空気抵抗を無視したニュートンの落下方程式を使えば、計算は簡単になるのだが、今回は生命にかかわるので厳密に空気抵抗を考慮に入れた方程式を使う。

ニュートンには “あっち” で謝っておきます。

 

落下の式は以下のとおり。

 

 
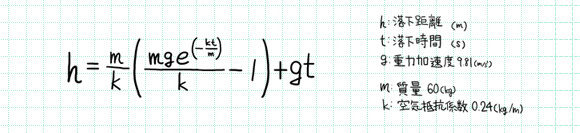
質量は60kg、空気抵抗係数は0.24を使用（空気抵抗係数はスカイダイビング時の値）

 

仮に３秒落下して地面に激突したければ、t=3として式をとけば、適切な高さは42mとわかる。
たとえば群馬県みなかみ町の諏訪峡大橋が42mである。ちなみにここではバンジージャンプが体験できる。

 

 

 

 

 

　「ボールがとまって見える」

 

巨人軍・川上哲治の言葉があるように、
人間の脳が高速化は、優れたアスリートならば知っている。
この何億倍の早送りが走馬灯ではおきていると考えればいい。

 

では、脳内の処理速度はどれくらいまで高速化するのか？

 

Verbal Lisa Taku（2000年発表）の「脳神経の処理速度と実時間比較の論文」、通称「 n-flow 」（ ニューラル・フロー )論文によると、1秒に処理できる脳内イベントは、時間にして、約11年と半年(11.574年)とある。

つまり、実時間の3億5600万倍 である。

 

 

これは、走馬灯の１年は、実際の0.0864秒ということになる。
つまり28年間全ての走馬灯を見るときの、実際の経過時間は、2.4秒 になる。

 

この方程式に照らし合わせれば、
私の人生は実時間でたったの2秒半で再現される計算だ。

人の一生とはそんなものか。
でも、巨人軍は永遠に不滅であります。

 

 

 

 

それでは、必要な落下距離を求めよう。

 

走馬灯が一生の追体験なら、年齢（享年）は走馬灯の体感時間に等しい。これは明白だ。
そして、n-flowを使って体感時間から実時間が求まる。

さらに実時間は落下時間と等しい。
そして落下時間から逆算して落下距離が求まる。
この落下距離が飛び降りる高さのことである。

 

長くなったが、

 自分の年齢から、何mから飛び降りたら走馬灯全部みれるかが求まる！！
 

湧き上がる興奮を抑えながら、
体感時間/実時間の変換式と、落下距離を求める式を組み合わせて解く。

 
どうぞ読み飛ばしてください。

 

 

 

マウスホイールをガーッ っとやっていた人も一旦、このへんで手を止めていただいて結論をみてもらいたい。

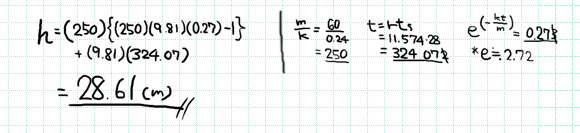
28才の人間の走馬灯に必要な高さは 28.61m。

マンションだったら9,10階建て くらい。
なかなかリアリティのある数字がでたのでびっくりしている。

 

 

 

 

 

この崖は、偶然にもジャスト 28.61m。今すぐにでもその計算結果の検証ができる。

 

 

 

私は、勇気を出して、

 

 

 

 

 

 

実験を……

 

 

 

 

 

 

敢行した……！

 

 

 

 

 

 

瞬間、死を悟った脳は高速に処理を始め、全ての動きが緩慢になり、突然、目の前が真っ暗になったかと思うと、突然光に包まれ……

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

走馬灯を見た。

 

……28年間の人生を、もう一度28年かけて追体験した。
実際の人生と同じく、長く、そしてリアルだった。

 

現実では、私は地面まであと何ミリというところまで落ちていることだろう。
時間にして0.01秒もないはず。そして本当にお別れがやってくる。

 

 

 

 

 

 

 

私が、走馬灯の中の「走馬灯」を見ている、と気が付いたのは、何度目の走馬灯を見ていたときだったのだろう。わからない。

 

走馬灯の中の最後、私は崖を飛び降りる。当然だ。走馬灯は人生の追体験なのだから。
そして、死を悟る。するとその走馬灯の中の私は走馬灯を見る。それの繰り返しだ。

 

 

 

 

 

 

20回、30回？人生を繰り返し、体感的には500年以上経っていた。
だが、まだ、現実の私の体は地面に激突していない。

 

一瞬の中に永遠がある。

 

 

 

 

一瞬の中の永遠、その意味が伝わるだろうか、

 

１，２，３，４，５，６，７，８，９,………

 

「10まで数えたら風呂から上がっていい」、そう言われて、９まで数えた。
しかし、言われる、「９と１０の間も数えなさい」、と。

 

 

9.1，9.２，9.３，9.４，9.５，9.６，9.７，9.８，9.９,………

 

 

9.9まで数えたあと、
言われるんだ、「９.9と１０の間も数えなさい」、と。

 

 

 

 

 

9.91，9.92，9.93………

 

 

200回、300回、合わせ鏡のように続く、同じ人生の走馬灯から抜け出す方法はなかった。
なぜなら、これは人生ではなく走馬灯で、私の人生は全て終わってしまっている。

 

 

私は、手出しすることも出来ずに、私の過去の選択を見ているだけだった。

 

 

 

 

 

9.991，9.992，9.993………

 

 

日常の些細な選択も、
後に人生を左右することになる岐路も、
そして飛び降りることも変わりなく、

私は、私がすることを黙ってみているよりなかった。

 

 

 

 

 

9.9991，9.9992，9.9993………

 

 

美しいが選択権の無い、眺めるだけの “虚像” 。それが走馬灯。
そこには、生まれては消えゆく、生命の残像があるだけだった……。

 

 

 

 

 

 

 

 

参考文献
アイルトン・セナは言っている：言ってません
諏訪峡大橋バンジージャンプ：みなかみバンジー
ボールがとまって見える：巨人軍、川上哲治
1日が100万年つまり1秒が約11年と半年：Hands/m-flo (2000/2/16)